The Golden Age
We may well be in the Golden Age of AI. Decades of theoretical promise are now blossoming into a new era of practical applications. While it is still arguable that AI applications lack true intelligence, the powerful capabilities, now made available to most of us, bring the technology closer to fulfilling its early potential.
Despite their sophisticated capabilities, the inner workings of AI algorithms are often surprisingly accessible. While a foundational understanding of college-level math and statistics is necessary, the core engineering principles behind these technologies are, with some effort, graspable for many. Even the more intricate aspects typically require only graduate-level math in specific situations. In essence, a strong software engineering background can provide a surprisingly thorough grasp of what goes on “under the hood” of many AI algorithms.
This blend of scientific theory and practical implementation makes AI a particularly fun and engaging area. The current state of the art allows you to experiment with a vast array of intriguing applications, but there are still boundless ways to tinker with and improve upon them.
NLP and Transformers
One topic I have been following closely is that of Natural Language Processing (NLP), which encompasses (among other areas) Siri and Alexa, translation functionality, predictive text (suggestions as you type), and chatbots like ChatGPT and Google Gemini.
NLP has been consistently improving for decades. But a significant breakthrough occurred in 2017 with the publication of the paper Attention is All You Need (AIAYN), and the invention of a new type of neural network architecture, the Transformer.
The writing style in technical papers, including in this particular one, tends to be dense and unapproachable, with quite a bit of jargon and equations. Fortunately, the more seminal works like this are often described in approachable articles and videos. For example:
- Attention is All You Need, Yannic Kilcher
- Attention is all you need (Transformer), Umar Jamil
- Attention is all you need, Eduardo Muñoz
Many more examples which cover the entire paper can be found, and far more which focus on key concepts. In my article here, I want to shed a little light on one of these ideas, that of Positional Encoding.
Positional Encoding
A significant reason for the improvement in transformer-based NLP applications is that they account for far more of the context (the other words in the sequence). Previous NLP architectures, such as RNNs and LSTMs, could consider some context, but had limitations, such as focusing on only a limited number of preceding words. Transformers use an attention mechanism which allows them to consider a large context surrounding a word, regardless of word order. Positional encoding augments this context by providing the (otherwise missing) explicit information regarding the spatial relationships between the words.
In other words, rather than providing the network with a bucket of words to be processed, positional encoding adds information about the spatial relationships between the words. This improves the network’s ability to understand the words, based upon their surrounding context.
For a trivial example, consider a network designed to translate between languages. If you feed it the two sequences of words “Scott bit the dog” and “The dog bit Scott”, you would hope that the network would discern the difference and produce different, appropriate output. The sets of words are identical, but their positioning is critical. This ordering information must be included in the input to guide the system to correct results.
Positional Encoding in Attention is All You Need (AIAYN)
In the case of AIAYN, the paper’s authors selected a fairly complex and obscure method for specifying the position information. This information is created by sampling a set of sinusoid (sine and cosine) curves of varying frequencies, in order to produce a vector of values. This vector is then added to that of the word itself, so that the word and its positional context are combined in a single vector.
A vector is used because the words themselves are encoded as numeric vectors rather than just strings or ids. This is done in a preprocessing step that takes very large text-based data sets (such as Wikipedia, the web, etc.), breaks the words into tokens, then feeds them into a neural network. The network uses contextual information such as nearby words to derive a set of weights with which it creates a vector of up to 1024 entries, known as a word embedding. Interestingly, this technique tends to form some sort of relationship between words. The topic of word embeddings is fascinating, and I may dive into it in more depth in a future post.
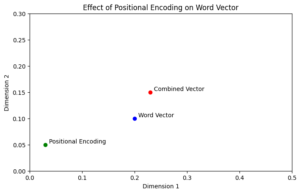
Figure 1: The effect of positional encoding on a word vector
One way of thinking of this is by imagining each word as a 2D point on a graph (Figure 1). Adding the positional encoding acts like a nudge, pushing the “word vector” in a direction specific to its context within the sentence. While actual word and positional embeddings have much higher dimensionality (far more than just two values), this analogy helps us grasp how their combination captures both a word’s meaning and its position in the sequence.
The aggregation of sampled curves into a vector is a bit weird. But don’t take my word for it. Watch these videos, where the creator easily describes the need for encoding and the formulas themselves but struggles multiple times to explain and justify the suggested mechanism:
Positional Encoding in Transformers
The Clock Analogy for Positional Encodings
The authors of AIAYN briefly mention in their paper that they experimented with other methods, but determined that this method works reasonably well in practice. However, there is very little background describing the suitability of the chosen algorithm in comparison to others.
Understanding the Rationale
Before diving into technical solutions, it’s crucial to understand the problem thoroughly. This allows for a clear evaluation of how well different techniques meet the specific requirements. Positional encoding is one of those topics where general descriptions and intricate mathematical details are readily available, but determining the rationale behind specific implementation choices, like using sampled sinusoids, can be challenging.
This sort of information gap is common in the software industry in general. It is not unusual for stakeholders to provide high-level requirements and have engineering teams immediately propose a specific solution. Too often, there are unspecified goals, ambiguous specifications, no process for choosing between alternative approaches, and no way of measuring suitability. I described one approach for considering and documenting engineering alternatives when I wrote about Spikes.
Understanding the reasoning behind the AIAYN positional encoding algorithm is particularly useful as the proposed solution is obscure and fairly complex.
The fundamental questions to ask include:
- What are the desired properties in a good positional encoding algorithm?
- How do these properties vary with the type of system under consideration?
- How do you evaluate position encoding algorithms?
- How should you choose between competing algorithms?
If you have information of this nature you can design or choose a good algorithm without guesswork or large amounts of experimentation. As a side benefit, this sort of background information can help you explain how your algorithm works. Explainability is a key topic in AI right now.
This is where it gets interesting, and current AI algorithm development can differ from product development. When developing products, we like to think that we are exploring new territory. But the work is rarely that innovative; if we take the time, we are usually able to create fairly complete specifications.
For fundamentally new algorithms often encountered in the AI space, the knowledge base is far less established. Here, we need to explore multiple potential solutions, comparing their properties and performance to identify what works best and, just as importantly, hypothesize why it does.
Once this information is determined, it is possible to create specifications and answer the fundamental questions.
In The Next Post
Fortunately, research into positional encoding has been consistent since the publication of AIAYN. In the next post, I’ll discuss a couple of approaches in a little detail, then attempt to discern what this says about better algorithms going forward.
